平均値と中央値の比較
ある確率分布からのサイズnのサンプルの標本平均と標本中央値の比較をシミュレーションしてみました。
n=11, 101, 1001の3パターン、分布は一様分布、正規分布、指数分布の3パターン、それぞれサンプリングして標本の平均と中央値をとるというのをN=1e+5回繰り返し、結果をヒストグラムにしたものがこちらです。
まずは一様分布です。nを増やすと横幅が狭くなって、高さがやや高くなっているでしょうか。
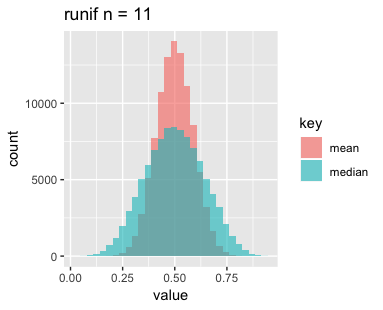
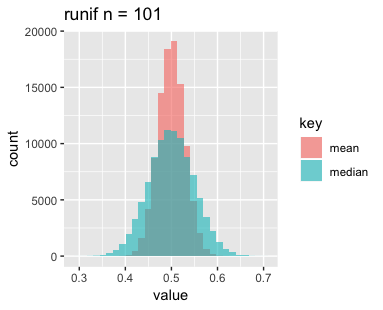
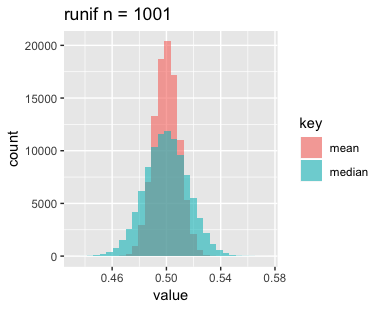
次に正規分布です。こちらもnを増やすと横幅が狭くなっていますが、高さはあまり変わっていないようです。


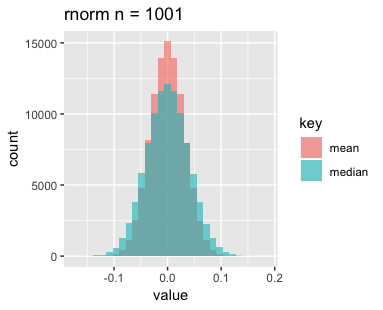
最後に指数分布です。nを増やすごとに平均と中央値がどんどんずれていくのが印象的です。指数分布が左右対称でないことに起因しているのでしょうか。
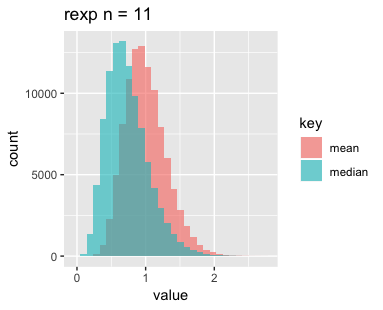
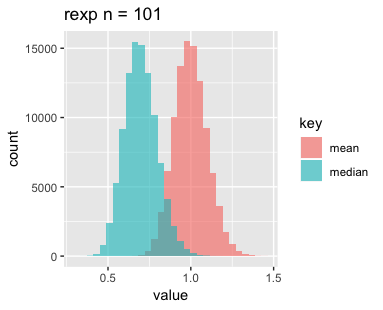
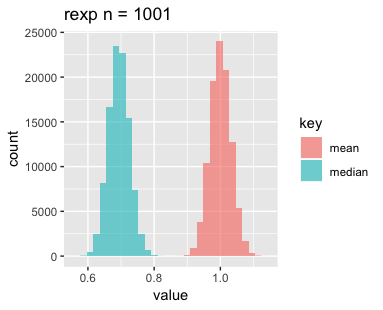
標本平均の分布については母平均の推定であったり中心極限定理であったりと比較的馴染みがありますが、中央値の分布については改めて可視化してみると面白いですね。今後はこれらがどのような分布になっているか調べてみようと思いますのでお楽しみに。
今回用いたRのコード及び同内容pythonのコードはこちらです。