標本平均と標本分散の分布
今回は標本の平均と分散がどのような分布になるかをシミュレーションします。
今回やりたいこと
標準正規分布に独立に従うサイズnの標本について、その平均と分散がどのような分布になるか、nを動かして調べます。
例えば以下のコードを実行すると、平均μ=0で標準偏差σ=1の正規分布からサイズn=5の標本をランダムにサンプルできます。
set.seed(123) mu <- 0 sigma <- 1 n <- 5 sample <- rnorm(n = n, mean = mu, sd = sigma)
すると、
> sample [1] -0.56047565 -0.23017749 1.55870831 0.07050839 [5] 0.12928774
となり、この平均と分散を計算すると、
> mean(sample) [1] 0.1935703 > var(sample) [1] 0.6577564
となります。
今回は、このsampleを生成する過程を繰り返しsampleの平均mean(sample)と分散var(sample)の値を集計した結果がどのような分布になるかを見ていきます。 またn=5以外にもn=10, 20, 50の場合にどのようになるかを見ていきます。
標本平均
まず標本平均の分布を調べます。 N=105回ランダムサンプリングしてデータを生成します。
d <- data.frame(mean = c(), var = c(), n = c()) N <- 1e+5 for(n in c(5,10,20,50)){ means <- c() vars <- c() for(i in 1:N){ sample <- rnorm(n = n, mean = mu, sd = sigma) means[i] <- mean(sample) vars[i] <- var(sample) } d <- rbind(d, data.frame(means, vars, n = as.factor(rep(n, N)))) }
これらについて、標本平均の分布を図示すると、
ggplot(data = d, aes(x = means, fill = n)) + geom_histogram(position = "identity", alpha = 0.5)

同じものを分割して表示すると
ggplot(data = d, aes(x = means, fill = n)) + geom_histogram() + facet_wrap( ~ n)

nを増加させると幅が狭くなりますが、いずれも0を中心に左右対称な形になります。
これらの平均と標準偏差は、
> d %>% + dplyr::select(means, n) %>% + dplyr::group_by(n) %>% + dplyr::summarise_all(funs(mean,sd)) # A tibble: 4 x 3 n mean sd <fct> <dbl> <dbl> 1 5 0.0000531 0.445 2 10 -0.00197 0.316 3 20 0.0000108 0.223 4 50 0.000201 0.142
です。平均はいずれのnでもおよそ0なのに対し、標準偏差はnが増加すると減少します。
この分布は実は正規分布になることがわかります。 いわゆる正規分布の再生性という性質です。このことについては次回以降詳しくみていきます。
標本分散
次に標本分散の分布です。 Rで計算されるのは(n-1)で割る方の不偏分散ですが、定数倍なので気にしないことにします。
上でサンプリングしたデータを用いて同様に図示していきます。
ggplot(data = d, aes(x=vars, fill = n)) + geom_histogram(position = "identity", alpha = 0.5)

同じものを分割して表示すると
ggplot(data = d, aes(x = vars, fill = n)) + geom_histogram() + facet_wrap( ~ n)

nを増加させると幅が狭くなり、さらにピークが右に寄っていきます。
これらの平均と標準偏差は、
> d %>% + dplyr::select(vars, n) %>% + dplyr::group_by(n) %>% + dplyr::summarise_all(funs(mean,sd)) # A tibble: 4 x 3 n mean sd <fct> <dbl> <dbl> 1 5 1.00 0.711 2 10 0.997 0.468 3 20 1.00 0.325 4 50 1.000 0.202
です。 平均はいずれのnでもおよそ1なのに対し、標準偏差はnが増加すると減少します。
この分布はχ二乗分布になることがわかります。こちらも次回以降詳しくみていきます。
まとめ
今回は標準正規分布から独立にサンプリングした標本の平均と分散がどのような分布になるのか、シミュレーションして可視化してみました。 次回以降、これらの分布についてより詳しく調べていきます。またそれを踏まえて区間推定や仮説検定について考えていきます。
今回用いたRのコードと同内容のpythonコードは以下にあります。
順序統計量とベータ分布 2
に引き続き、順序統計量の分布について調べていきます。
この記事の目標は、一様分布に独立に従うサイズnの標本のp番目の値がどのような分布に従うかを計算することです。
順序統計量とは
順序統計量というのは、標本におけるある順位の値のことです。例えば、最大値や最小値、中央値などがそれに当たります。 より一般には、サイズ10の標本のうち小さい方から3番目のデータがどのような分布になるか?などを考えます。
はじめにサイコロの出る目についての問題を考え、そのあとで目標である一様分布の場合を考えます。サイコロの問題は一様分布の離散版と考えることができます。
サイコロの場合
4個のサイコロを振って小さい順から2番目の目が2以下である確率を計算してみましょう。これは、4個全てが2以下、4個中3個だけが2以下、4個中2個だけが2以下という3つの排反なパターンに分けることができます。それぞれの確率は
- (2/6)4
- 4 * (2/6)3 * (4/6)
- 4C2 * (2/6)2 * (4/6)2
となり、合計すると11/27となります。
同様に4個中2番目がx以下である確率は
- (x/6)4
- 4 * (x/6)3 * (1-x/6)
- 4C2 * (x/6)2 * (1-x/6)2
となり、合計するとx2(3x2-8x+6)/64となります。
さらに一般化して、4個中p番目がx以下である確率は、4個中4個がx以下から4個中p個だけがx以下までの4-p+1通りの排反なパターンに分けることができます。4個中k個だけがx以下である確率は
- 4Ck * (x/6)k * (1-x/6)4-k
となり、合計するととなります。
最後にn個中p番目がx以下の場合もやっておきましょう。n個中p番目がx以下である確率は、n個中n個がx以下からn個中p個だけがx以下までのn-p+1通りの排反なパターンに分けることができます。n個中k個だけがx以下である確率は
- nCk * (x/6)k * (1-x/6)n-k
となり、合計すると
$$ \sum_{k=p}^n {}_nC_k \frac{x}{6}^k (1-\frac{x}{6})^{n-k} $$
となります。
一様分布の場合の例
0以上1以下の一様分布に従う独立な確率変数X_1, X_2, X_3, X_4の2番目の値が0.3以下である確率は、
- 4個全て0.3以下であるのが0.34
- 4個中3個だけが0.3以下であるのが4 * 0.33 * 0.7
- 4個中2個だけが0.3以下であるのが4C2 * 0.32 * 0.72
であり、それの合計です。
同様に4個中2番目がx以下である確率は、
- 4個全てx以下であるのがx4
- 4個中3個だけがx以下であるのが4x3 (1-x)
- 4個中2個だけがx以下であるのが4C2 x2 (1-x)2
となり、これの和が分布関数です。
確率密度関数はこれのxでの微分です。和をとる前に各項の微分を計算しておくと、それぞれ
- 4 x3
- 4 3x2 (1-x) + 4 x3 (-1) = 4 3x2 (1-x) - 4 x3
- 4C2 * 2x (1-x)2 + 4C2 x2 * (-2)(1-x) = 4C2 * 2 x (1-x)2 - 4 * 3 x2 (1-x)
となります。これを足すと、打ち消しあう項があるので、
$$ 4 x^3 + (4 \times 3x^2 (1-x) - 4 x^3) + ({}_4C_2 2x(1-x)^2 - 4 \times 3 x^2 (1-x)) = {}_4C_2 2x(1-x)^2 $$
となります。
この結果をシミュレーションと比較してみましょう。
library(dplyr) library(ggplot2) compare <- function(N,n,p,fun){ x <- c() for(i in 1:N){ x[i] <- sort(runif(n))[p] } data.frame(x=x) %>% ggplot(aes(x=x)) + geom_histogram(aes(y=..density..), fill = 'royal blue', binwidth = 0.05, boundary = 0) + stat_function(fun=fun) + labs(title = paste("n =",as.character(n),", p = ",as.character(p))) } N <- 1e+5 n <- 4 p <- 2 fun <- function(x) 12*x*(1-x)**2 compare(N,n,p,fun)
を実行すると、

となります。
一般的な状況
最後により一般に、一様分布に独立に従う標本の順序統計量の確率密度関数を計算してみます。
0以上1以下の一様分布に従う独立な確率変数X_1, ..., X_nのp番目の値がx以下である確率は、
- n個全てx以下であるのがxn
- n個中n-1個だけがx以下であるのがn xn-1 (1-x)
- n個中k個だけがx以下であるのがnCk xk (1-x)n-k
- n個中p個だけがx以下であるのがnCp xp (1-x)n-p
の和が分布関数です。
上と同様に確率密度関数はこれのxでの微分です。和をとる前に各項の微分を計算しておくと、それぞれ
- n xn-1
- n(n-1) xn-2 (1-x) - n xn-1
- nCk k xk-1 (1-x)n-k - nCk(n-k) xk (1-x)n-k-1
- nCp p xp-1 (1-x)n-p - nCp(n-p) xp (1-x)n-p-1
となります。これを足すと、打ち消しあう項があるので、
$$ n x^{n-1} + (n(n-1)x^{n-2} (1-x) - n x^{n-1}) \\ + ({}_nC_2 (n-2)x^{n-3}(1-x)^2 - n(n-1)x^{n-2} (1-x)) \\ + \cdots \\ + ({}_nC_p px^{p-1}(1-x)^{n-p} - {}_nC_p(n-p)x^p (1-x)^{n-p-1}) \\ = {}_nC_p px^{p-1}(1-x)^{n-p} $$
となります。これがいわゆるベータ分布です。
前回冒頭で紹介したケースでシミュレーションと比較してみましょう。 サンプルサイズn=10でp=3とすると、密度関数は上の計算結果から
$$ {}_{10}C_33x^2 (1-x)^7 $$
となります。
library(dplyr) library(ggplot2) compare <- function(N,n,p,fun){ x <- c() for(i in 1:N){ x[i] <- sort(runif(n))[p] } data.frame(x=x) %>% ggplot(aes(x=x)) + geom_histogram(aes(y=..density..), fill = 'royal blue', binwidth = 0.05, boundary = 0) + stat_function(fun=fun) + labs(title = paste("n =",as.character(n),", p = ",as.character(p))) } N <- 1e+5 n <- 10 p <- 3 fun <- function(x) (10*9*8)/2*x**2*(1-x)**7 compare(N,n,p,fun)
を実行すると、

まとめ
まとめると、一様分布に独立に従うサイズnの標本のp番目の値が従う分布の確率密度関数は
$$ {}_nC_p px^{p-1}(1-x)^{n-p} $$
であり、これはベータ分布と呼ばれる確率分布と一致することがわかりました。 今回用いたコードは前回と同じものです。
順序統計量とベータ分布
の続きで、標本の中央値の分布がどのようになるかを調べていきます。 また、より一般に順序統計量というものについて調べます。
順序統計量というのは、標本におけるある順位の値のことです。例えば、最大値や最小値、中央値などがそれに当たります。 より一般には、サンプルサイズ10のサンプルのうち3番目のデータがどのような分布になるか?などを考えます。
特に今回と次回は0以上1以下の一様分布から独立なサイズnのサンプルを取った時、そのp番目のデータがどのような分布を持つかを調べていきます。
シミュレーション
まずは実験してみましょう。
例えば、サンプルサイズn=10の標本のうち小さい方からp=3番目の値がどのような分布になるかをシミュレーションしてみます。
set.seed(123) runif(10)
を実行すると
[1] 0.2875775 0.7883051 0.4089769 0.8830174 0.9404673 [6] 0.0455565 0.5281055 0.8924190 0.5514350 0.4566147
と乱数が生成され、これの3番目の値は0.37053701です。
もう一度
runif(10)
を実行すると
[1] 0.95683335 0.45333416 0.67757064 0.57263340 [5] 0.10292468 0.89982497 0.24608773 0.04205953 [9] 0.32792072 0.95450365
と乱数が生成され、これの3番目の値は0.24608773です。
この3番目の値をとる、というのをN=100000回繰り返してヒストグラムを描いてみます。
ord_sampling <- function(N,n,p){ x <- c() for(i in 1:N){ x[i] <- sort(runif(n))[p] } data.frame(x=x) %>% ggplot(aes(x=x)) + geom_histogram(binwidth = 0.05, boundary = 0, fill = 'royal blue') + labs(title = paste("n =",as.character(n),", p = ",as.character(p))) } runif(10) N <- 1e+5 n <- 10 p <- 3 ord_sampling(N,n,p)

おおよそ0.2から0.25あたりの値が最頻で、直感にはまあ合う結果でしょう。
他にも、同じようにサンプルサイズn=10の標本のうち小さい方からp=1,2,4,5番目の値がどのような分布になるかをシミュレーションしてみます。




先に答えを言ってしまうと、実はこれはベータ分布と呼ばれる分布になっています。 このことを確率密度関数を計算することで確かめていきましょう。
今回は小手調べでサンプルサイズn=2の時に、最小値の分布がどのような確率密度関数を持つのかを計算してみます。
確率密度関数を計算するには、分布関数を求め、その微分を計算する必要があります。 ここでは分布関数は、xに対してサンプルの最小値がx以下である確率を与える関数です。 今回は、サンプルX1, X2が一様分布U(0,1)に独立に従う確率変数で考えます。 そのうち小さい方(正確には大きくない方)がx以下である確率を計算してみましょう。
サイコロの場合
一様分布の場合を計算する前に、より単純な設定でサイコロの出目についての問題を考えてみます。 サイコロ二つを振って小さい方(正確には大きくない方)が2以下である確率を計算してみましょう。
サイコロ二つの名前を1番と2番とし、1番の目をX1とし、2番の目をX2とします。 これらは確率変数で、1から6までの値を1/6ずつの確率でとります。 X1が2以下になる確率は2/6で、X2が2以下になる確率も2/6です。
最小値が2以下になる確率は、
- X1が2以下でX2が3以上になる確率2/6 * (1-2/6) = 8/36
- X1が3以上でX2が2以下になる確率(1-2/6) * 2/6 = 8/36
- X1もX2も両方2以下である確率2/6 * 2/6 = 4/36
の合計なので、20/36となります。 これは二つの出目の36通りのうち、条件に該当するものがどちらかが1または2である20通りであることからも計算できます。
同様に小さい方がx以下である確率は次のように計算できます。 X1が2以下になる確率はx/6で、X2が2以下になる確率もx/6です。 最小値がx以下になる確率は、
- X1がx以下でX2がx+1以上になる確率x/6 * (1-x/6) = x/6 - x2/36
- X1がx+1以上でX2がx以下になる確率(1-x/6) * x/6 = x/6 - x2/36
- X1もX2も両方x以下である確率x/6 * x/6 = x2/36
の合計なので、2x/6 - x2/36となります。この結果はどちらかがx以下であるパターンの数え上げで2xから共通部分のx2を引いたものとしても計算できます。
一様分布の場合
さて、上のサイコロと同様の計算を行います。 サンプルとして与えられる二つの値を確率変数X1, X2とします。 これらは独立に一様分布U(0,1)に従う確率変数であり、X1がx以下である確率はxであり、X2がx以下である確率も同じくxです。
最小値がx以下になる確率は、
- X1がx以下でX2がx以上になる確率x * (1-x) = x - x2
- X1がx以上でX2がx以下になる確率(1-x) * x = x - x2
- X1もX2も両方x以下である確率x * x = x2
の合計なので、2x - x2となります。これが分布関数です。 さらにこれを微分すると2-2xで、これが密度関数です。
最後にシミュレーション結果と、上で求めた密度関数のグラフを重ねて表示してみましょう。
compare <- function(N,n,p,fun){ x <- c() for(i in 1:N){ x[i] <- sort(runif(n))[p] } data.frame(x=x) %>% ggplot(aes(x=x)) + geom_histogram(aes(y=..density..), fill = 'royal blue', binwidth = 0.05, boundary = 0) + stat_function(fun=fun) + labs(title = paste("n =",as.character(n),", p = ",as.character(p))) } N <- 1e+5 n <- 2 p <- 1 fun <- function(x) 2*(1-x) compare(N,n,p,fun)

このように、上で計算した関数2-2xのグラフと、サンプリングした結果のヒストグラムがおおよそ一致していることが確認できます。 次回はより一般のケースを計算してみますのでお楽しみに。
今回用いたRのコード及び同様のpythonのコードは以下です。
平均値と中央値の比較
ある確率分布からのサイズnのサンプルの標本平均と標本中央値の比較をシミュレーションしてみました。
n=11, 101, 1001の3パターン、分布は一様分布、正規分布、指数分布の3パターン、それぞれサンプリングして標本の平均と中央値をとるというのをN=1e+5回繰り返し、結果をヒストグラムにしたものがこちらです。
まずは一様分布です。nを増やすと横幅が狭くなって、高さがやや高くなっているでしょうか。
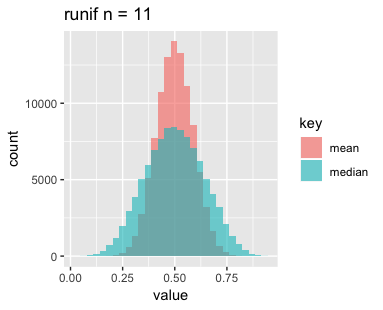
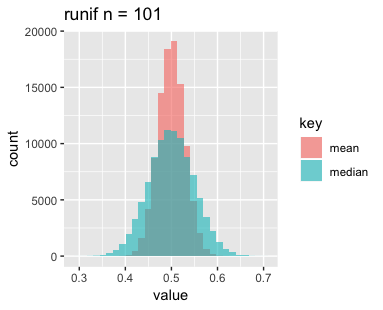
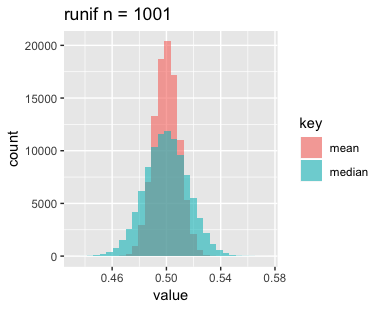
次に正規分布です。こちらもnを増やすと横幅が狭くなっていますが、高さはあまり変わっていないようです。


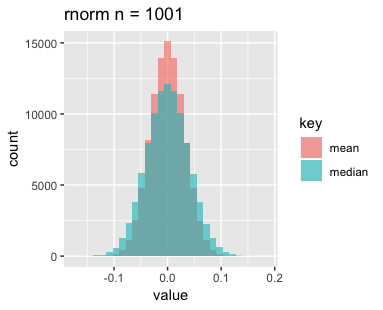
最後に指数分布です。nを増やすごとに平均と中央値がどんどんずれていくのが印象的です。指数分布が左右対称でないことに起因しているのでしょうか。
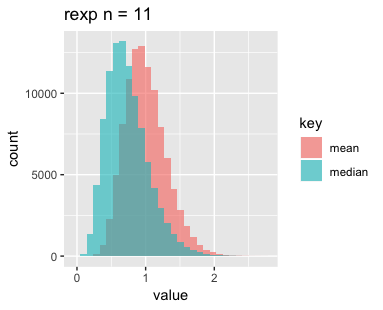
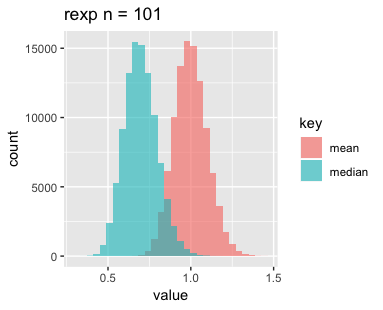
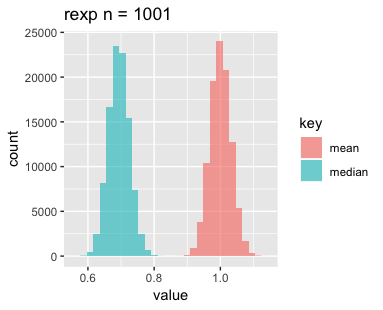
標本平均の分布については母平均の推定であったり中心極限定理であったりと比較的馴染みがありますが、中央値の分布については改めて可視化してみると面白いですね。今後はこれらがどのような分布になっているか調べてみようと思いますのでお楽しみに。
今回用いたRのコード及び同内容pythonのコードはこちらです。
検索量を用いた状態空間モデルによる売上予測
この記事はStan Advent Calendar 2018
の23日目の記事です。本記事では状態空間モデルを用いた時系列予測について実データでの分析例を紹介します。
2015年度人工知能学会全国大会(第29回)での論文、
状態空間モデルを用いた検索トレンドとページビューからの自動車販売台数の予測, 角田 孝昭, 吉田 光男, 津川 翔, 山本 幹雄
と同内容の状態空間モデルによる予測をStanを用いて行ってみました。この論文では、自動車の販売台数の月次データの予測を状態空間モデルを用いて行っていて、説明変数として絵googleの検索量を用いることで予測が改善するかどうかを調べています。
使用データについて
今回使用したデータは論文と同様に日本自動車販売協会連合会
からとってきた車種ごとの月次販売台数データと、Googleトレンドからとってきた検索量のデータです。 販売台数データについてはpdfファイルから
を参考に取り出しました。データを取り出す過程もいろいろ面倒なところがあったのですが、これについては記事を改めて紹介したいと思います。
予測モデルについて
状態空間モデルについては本Advent Calenderでの
をご覧ください。簡単に紹介すると、時系列のようなデータに対して、その観測値を直接予測するのではなく状態という観測できない隠れた変数を用意し、状態についての時系列モデルに加えて状態にノイズを乗せて観測値が得られるというモデルです。
もっともシンプルなモデルとしては、
というものがあります。
ここで、
- tが時刻
- ytが観測値
- vtが観測誤差
- μtが状態
- wtが状態の変動
を表します。このwtやvtが正規分布に従うと仮定すると、μはランダムウォークになります。つまり、一時点前の状態μt-1に正規分布から発生した量wtが加わることで、時刻tでの状態μtが得られるというのが状態のモデルです。さらにこの状態から、正規分布から発生した誤差が加わったことで観測値ytが得られるというのが状態空間モデルです。推定するパラメータは状態μt、及び観測誤差wtや状態変動vtの分散で、これらを推定したうえでytを予測します。
今回のコードについては上記の松浦さんの本に同じような状態空間の例がありましたので、そちらを参考にさせていただきました。本で用いられているコードは
にありますので、そちらもご参照ください。また結果の図示については
を参考にしました。(もし問題がある場合にはお知らせ下さい。)
元論文ではいくつかの車種について実験を行なっていますが、今回は販売台数一位のノートのみを用いています。
まずは論文のベースラインモデルですが、2階差分トレンドで12ヶ月周期の季節項入りのモデルを、松浦さんの本にちょうど同じものがあったので、参考にしました。
モデルの式は以下の通りです。
で、
- ytが販売台数の観測値
- γy,tが販売台数の季節成分
- μy,tが販売台数のトレンド
- vtが販売台数の観測誤差
- wtが販売台数のトレンドの変動
です。
次に提案モデルですが、こちらは検索量も2階差分の季節成分入りのトレンドモデルを用いて状態を予測し、販売量の状態に一次式で説明変数として検索量のトレンド成分を加えるというものです。
モデルは少々複雑ですが以下の通りです。
これは検索量についての状態空間モデルと販売台数についての状態空間モデルの組み合わせです。
- xtが検索量の観測値
- γx,tが検索量の季節成分
- μx,tが検索量のトレンド
- vx,tが検索量の観測誤差
- wx,tが検索量のトレンドの変動
というのが下二つの式に現れる変数で、こちらが検索量についての季節成分入り2階差分トレンドモデルになっています。
- ytが販売台数の観測値
- γy,tが販売台数の季節成分
- μy,tが販売台数のトレンド
- bが販売台数への検索量の影響の重み
- vy,tが販売台数の観測誤差
- wy,tが販売台数のトレンドの変動
というのが上二つの式に現れる変数です。こちらも同様に季節成分入り2階差分トレンドモデルですが、販売台数の観測値の式に検索量の状態が説明変数として加わっていることに注意してください。
モデル部分のStanコードはこんな感じです
model {
alpha_X[3:N] ~ normal(2*alpha_X[2:(N-1)] - alpha_X[1:(N-2)], s_a_X); //検索量トレンドの状態モデル
for(t in 12:N){
season_X[t] ~ normal(-sum(season_X[(t-11):(t-1)]), s_season_X); //検索量季節成分
}
X ~ normal(x_mean, s_X); //検索量の観測モデル
alpha_Y[3:N] ~ normal(2*alpha_Y[2:(N-1)] - alpha_Y[1:(N-2)], s_a_Y); //販売台数トレンドの状態モデル
for(t in 12:N){
season_Y[t] ~ normal(-sum(season_Y[(t-11):(t-1)]), s_season_Y); //販売台数季節成分
}
Y ~ normal(y_mean + b * alpha_X, s_Y); //販売台数の観測モデル
}
またそのバリエーションとして、検索量を同じ月のものではなく1月前にしたもの、2期前にしたもの、また2期前までの3期分を使ったもの、の3種類のモデルを考えます。
モデルの式はそれぞれ以下の通りです。
このモデルでは、一期前の検索量のトレンド成分を説明に用いるので、μx,t-1がytの式に入っています。
このモデルでは、二期前の検索量のトレンド成分を説明に用いるので、μx,t-2がytの式に入っています。
このモデルでは、二期前までの検索量のトレンド成分を説明に用いるので、μx,t, μx,t-1, μx,t-2の三つがytの式に入っています。
予測結果について
学習データとして2014/1から2017/6までのデータを使い、2017/7から2018/6までをテストデータとしています。これを用いてStanによりMCMCサンプリングした結果のRhatをmcmc_rhatでプロットしたもの以下の通りです。





複数期のトレンド成分を用いたモデルは収束が悪いですが、今回はここを改善する時間がなかったのでこのままとします。
また時系列での予測のプロットは以下の通りです。





太い線が実際のデータで細い線がサンプリングした結果の中央値です。また, 色の濃い部分が10%から90%の範囲、薄い部分が2.5%から97.5%です。ベースラインモデル以外では、学習データの部分で実際の値と予測値の中央値が少しずれている部分があるのが気になります。
これらのモデルの予測の評価を行いましょう。元論文ではカルマンフィルタにより予測値を計算しそれと実際の値の誤差二乗和を計算していますが、今回はStanでサンプリングした予測値の平均値とテストデータとの誤差二乗和で評価を行います。また、元論文では相対的な誤差を計算していますが、今回は1車種しか予測しないので、そのままの値で計算します。
それぞれのモデルで誤差を計算した結果は以下の通りです。
- ベースラインモデルが349,513,623
- 提案モデルが306,010,351
- 一期前モデルが125,867,523
- 二期前モデルが397,689,428
- 複数期モデルが1,633,516,793
となっており、一期前の検索量を入れたモデルがもっともよく予測できているという結果でした。
他の車種も含めた分析であったり、他のモデルを試してみたり、またモデル比較についても交差検証やWAIC, WBICその他の指標を用いるなどいくつか試してみたいことはありますので、また実験してみたいと思います。最後までお付き合いありがとうございました。
なお、今回分析で用いたコードは以下にあります。
もし誤りや、改善点などお気付きでしたらお知らせいただけると幸いです。
Edwardをさわってみた
こちらはTensorFlow Advent Calendar 2017 - Qiita14日目の記事です。
今年何度かEdwardという単語を目にして、気になっていたのでさわってみることにしました。Edwardについては、以下のスライドで紹介されています。
公式ページはこちらです。
tensorflowについても初心者なこともあって、公式のTutorialも難しいと感じました。
そこで以下のgithubのページのコード例を参考に二項分布のパラメータ推定を書いてみようというのがこの記事です。
edward/examples at master · blei-lab/edward · GitHub
APIページを見ながら、Data, Model, Inference, Criticismという流れに沿ってコードを書いていきます。
まずはDataです。
Dataはnumpyのarrayやtensorflowのtensorで与えます。
今回はコイン投げ4回分の結果が与えられたものとします。表が1で裏が0ということにしましょう。
ここではデータを適当に手で与えます。
後のメソッドに渡すときに、データの形を合わせないとうまくいかなかったのでreshapeしてあります。
# DATA n = 4 x_train = np.array([0, 1, 1, 1]).reshape((n,1))
次にModelを記述します。
ここでは確率変数を定義します。
確率変数xがサンプル数n=4で確率pの二項分布にしたがい、確率変数pはベータ分布Beta(1,1)に従うとしています。
pの方は事前分布ということでしょうか。
# MODEL alpha = 1.0 beta = 1.0 p = Beta(concentration1=tf.Variable([alpha]),concentration0=tf.Variable([beta])) x = Bernoulli(probs=p, sample_shape=(n))
次にInferenceです。Inferenceには大きく分けてVariational Inference, Monte Calro, exactの三種類あり、exactは共役分布を用いて解析的に事後分布を求めるものです。
今回の二項分布、ベータ分布のモデルでは共役分布を用いた推定及びMonte Carloを用いた推定が
edward/examples at master · blei-lab/edward · GitHub
のbeta_bernoulli.py, beta_bernoulli_conjugate.pyにあるので、Variational Inferenceを試してみました。
ここではパラメータの事後分布を表す確率変数を定義します。 今回はパラメータの確率変数pに対して事後分布の確率変数qpを定義するのですが、まずはMAP推定をするために一点のみ確率1でとる分布を設定します。
Inferenceのためのメソッドには、引数としてパラメータの確率変数と事後分布の確率変数、データの確率変数と実際のデータをdict形式で渡します。
データの確率変数xに対して実際のデータx_trainを与えます。
# INFERENCE by MAP qp = PointMass(params=tf.Variable([0.1])) inference = ed.MAP({p: qp}, data={x: x_train}) inference.run()
ここでqpにパラメータを設定しているのですが、これがどういうことなのかまだ理解できていません。 MAP推定なので事後分布の最大値を求めるわけですが、その過程で必要になるということでしょうか。
最後にCriticismです。 結果を見ます。
# CRITICISM sess = ed.get_session() print(sess.run(qp.mean())) print(sess.run(qp.params)) print(qp.eval())
値はどれで見ても0.8124になります。 事前分布がBeta(1.0, 1.0)であればMAP推定量は今回だと0.75になるはずなので、何か違うのかもしれません。
x_post = ed.copy(x, {p: qp})
print(ed.evaluate('binary_accuracy', data={x_post: x_train}))
こちらは0.75になります。 事後分布で予測すると正解率が0.75になるということのようです。
x_trainを別のデータに置き換えると正解率は変わりますが、その都度乱数を発生しているということではなさそうです。 Variational Inferenceの別のメソッドとしてKallback Leibler divergenceを用いた変分推定も試してみます。
# INFERENCE by KLqp alpha = 1.0 beta = 1.0 qp = Beta(concentration1=tf.Variable([alpha]),concentration0=tf.Variable([beta])) inference = ed.KLqp({p: qp}, data={x: x_train}) inference.run()
こちらも結果を見ます。
# CRITICISM sess = ed.get_session() print(sess.run(qp.mean())) print(sess.run(qp.concentration0), sess.run(qp.concentration1)) print(qp.eval())
出力は
[ 0.64722526]
[ 2.47322822] [ 4.53755856]
[ 0.91249388]
となります。
qp.eval()は乱数を発生しているようです。
単純に事後分布を計算するとBeta(2.0, 5.0)になるはずですが、それと比べると推定できていると言えるでしょうか。
x_post = ed.copy(x, {p: qp})
print(ed.evaluate('binary_accuracy', data={x_post: x_train}))
こちらは0.25となりました。
ちゃんとコードを動かすだけでもなかなか時間がかかりましたが、ひとまず動いたのでこれからも色々試していきたいと思います。
今回のコードは以下にあります。
WAICとWBICによる混合Gauss分布のモデル選択
Stan Advent Calendar 2017 - Qiitaの12/7の記事です。
Stanによる混合Gauss分布のパラメータ推定のモデル選択をWAIC及びWBICで行なってみます。
上記の記事で1次元の場合にされていることを今回は2次元でやってみました。
WAICやWBICについては上記記事や、渡辺先生による以下のページをご覧ください。
http://watanabe-www.math.dis.titech.ac.jp/users/swatanab/waicwbic.html
http://watanabe-www.math.dis.titech.ac.jp/users/swatanab/waicwbic_j.html
今回扱うデータを生成する分布は
- 平均は等しく、x方向とy方向で分散が異なる二つの正規分布からの混合分布
でやりたかったのですが、平均を等しくすると収束がうまくいかなかったので、少し平均をずらした二つの正規分布の混合分布としました。
実際には
- 平均(0.1, 0)で共分散行列が(2, 0 \\ 0, 0.1)の正規分布と平均(0, 0.1)で共分散行列が(0.1, 0\\ 0, 2)である正規分布の混合比率1:1の混合分布
でデータを生成しています。
これを
- model2:クラスタ数2の混合分布モデル、ただし混合比率は0.5で固定
の2通りで平均、分散を推定し、データを複数回生成した上でWAICとWBICの分布の様子、及びモデル選択の結果を調べます。
サンプル数としてはN=30, 100の2通りで実験してみました。
サンプル数30ではmodel2の収束がなかなかうまくいっていないことも多いです。
事前分布を設定することでうまく収束させることもできるかもしれませんが、今後試してみます。
WAIC, WBIC及びモデル選択の結果は以下の通りです。
まずサンプル数30で100回試行した結果
- WAICではmodel1が49回
- WBICではmodel1が43回
サンプル数100で50回試行した結果
- WAICではmodel1が12回
- WBICではmodel1が7回
選択されるという結果となりました。
それぞれの分布の様子は以下のようになりました。


今回用いたコードは以下のものです。WAICやWBICを計算する部分は、上記記事のものを参考にさせていただきました。
gist308edbde04b774e49287026a0a969b16
本記事を書くにあたり、上記記事に加えちょうど一年前の同じ日にStan Advent Calendarに書かれた以下の記事も参考にさせていただきました。
また混合分布のコードを書くにあたっては、stanのmanualも参考にしました。
本記事では実験した結果の報告のみですが、別のケースで実験したり理論的な部分も含めて今後は考察していきたいと思っています。